Home
Giáo dục đào tạo
Tài liệu, đề thi THPT các trường
Tài liệu ôn thi THPT Quốc gia Chuyên đề Đạo hàm
Tài liệu ôn thi THPT Quốc gia Chuyên đề Đạo hàm
CHUYÊN ĐỀ: ĐẠO HÀM
BUỔI 1:
ĐỊNH NGHĨA ĐẠO HÀM VÀ QUY TẮC TÍNH ĐẠO HÀM
A. KIẾN THỨC CƠ BẢN
1. Định nghĩa đạo hàm:
Đạo hàm của
)(xf
tại
0
x
, kí hiệu
)(
0
'
xf
hay
)(
0
'
xy
0
'0 0 0
0x 0 x x 0
f (x x) f (x ) f (x) f (x )
f (x ) lim lim
x x x
2. Quy tắc tính đạo hàm và công thức tính đạo hàm
*Các quy tắc : Cho
; ; :u u x v v x C
là hằng số .
' ' 'u v u v
. ' '. '. . .u v u v v u C u C u
2 2
'. '. .
, 0
u u v v u C C u
v
v u
v u
Nếu
, .
x u x
y f u u u x y y u
.
*Các công thức :
0 ; 1C x
1 1
. . . , , 2
n n n n
x n x u n u u n n
1, 0 , 0
2 2
u
x x u u
x u
B. KĨ NĂNG CƠ BẢN
* Các bước tính đạo hàm bằng định nghĩa:
+ Bước 1: Giả sử ∆x là số gia của đối số tại xo.
Tính ∆y = f(xo + ∆x) – f(xo).
+ Bước 2: Tính
o
x x
y
lim x
suy ra f′(xo)
*Công thức tính đạo hàm nhanh của hàm hữu tỉ :
Dạng : y =
'''
2
2
cxbxa
cbxax
y’ =
22
2
)'''(
)''()''(2)''(
cxbxa
cbbcxcaacxbaab
Dạng : y =
edx
cbxax
2
y’ =
2
2
)(
)(.2.
edx
dcbexaexad
Dạng : y =
dcx
bax
y’ =
2
)( dcx
cbad
C. BÀI TẬP LUYỆN TẬP
Bài toán 1: Tính đạo hàm bằng định nghĩa:
Bài tập 1: Tính (bằng định nghĩa) đạo hàm của mỗi hàm số sau:
a) y = x2 + x tại
1
0x
b) y =
1
1
x
x
tại
0
0
x
Lời giải
a) y = x2 + x tại
1
0x
Gọi
x
là gia số của x tại
1
0x
Ta có
)()( 00 xfxxfy
xxxxxxxfxf 321212)1()1()1()1(
222
3)1('
3)3(lim
)3(
lim
3
limlim 00
2
00
f
x
x
xx
x
xx
x
y
xxxx
b) y =
1
1
x
x
tại
0
0
x
Gọi
x
là gia số của x tại
0
0
x
Ta có
)()( 00 xfxxfy
1
2
1
1
1
)1(
1)0(
1)0(
)0()0(
x
x
x
x
x
x
fxf
2)0('
2
1
2
lim
)1(
2
lim
1
.
1
2
limlim
0000
f
xxx
x
xx
x
x
y
xxxx
Nhận xét: Để tính hàm số y =
)(xf
trên khoảng (a;b) và
);(
0
bax
bằng định nghĩa ta chỉ
cần tính
)()( 00 xfxxfy
sau đó lập tỉ số
x
y
rồi tìm giới hạn của
x
y
khi
x
tiến dần về 0.
Bài toán 2: Tính đạo hàm của hàm số theo quy tắc
Dạng 1: Tính đạo hàm của Tổng, Hiệu, Tích, Thương.
Bài tập 2: Tính đạo hàm của các hàm số sau:
a)
3
1
2
5
x
xy
b)
125
235
xxxy
c)
4
32
x
x
y
d)
)133)(29(
2
xxxy
Lời giải:
a)
3
1
25 x
xy
2
4
2
4
'
'
'
5
'
5
1
10
1
103
1
23
1
2' x
x
x
x
x
x
x
xy
b)
125
235
xxxy
xxxxxxxxxy 4155)1('25'125'
24'2
'
35235
'
c)
4
32
x
x
y
2222
''
'
'
)4(
11
)4(
3282
)4(
)32()4(2
)4(
)32()4()4()32(
4
32
xx
xx
x
xx
x
xxxx
x
x
y
d)
)133)(29(
2
xxxy
)29)(36()133(2
)29()133()133()29(
)13
2
3)(29(
2
'22'
'
'
xxxx
xxxxxx
xxx
y
610
4
2
5
5
'
5
'
105
2
)'(
2
1
2xx
x
x
x
x
y
296618
6271254266
2
22
xx
xxxxx
Nhận xét: Để tìm đạo hàm của hàm số
)(xfy
ta chỉ cần xác định dạng của hàm số rồi
áp dụng các công thức và phép toán của đạo hạm để tính đạo hàm của hàm số.
Dạng 2: Tính đạo hàm của hàm hợp
Bài tập 3: Tính đạo hàm của các hàm số sau:
a)
19944 )342( xxy
; b)
122
2
xy
; c)
5
2
x
y
d)
3
25
22 xxy
Lời giải:
a)
19944 )342( xxy
' 4 1993 4 '
4 1993 3
y 1994(2x 4x 3) (2x 4x 3)
1994(2x 4x 3) (8x 4)
b)
122
2
xy
)12
4
)122
)12(
2
22
'2
'
x
x
x
x
y
c)
5
2
x
y
d)
3
25
22 xxy
2
2
2215
22
)2(
22215
22223
22223
22
2
4
2
25
2
'2
4
2
25
'
2
'
5
2
25
'
25
2
25
'
3
25'
x
x
xxx
x
x
xxx
xxxx
xxxx
xxy
Bài toán 3: Giải bất phương trình.
Phương pháp giải: Để giải bất phương trình ta làm các bước sau:
Bước 1: Tính đạo hàm của hàm số
)(xf
và
)(xg
(nếu có)
Bước 2: Xác định điều kiện bất phương trình rồi thay
)(
'xf
và
)(
'xg
(nếu có) vào điều kiện tìm
nghiệm
0
x
Bước 3: Lập bảng xét dấu rồi kết luận tập nghiệm của bất phương trình.
Bài tập 4: Giải các bất phương trình sau:
a)
)(
'xf
< 0 ,với
xxxxf 6
2
5
3
1
)(
23
b)
0)(
'xg
,với
2
93
)(
2
x
xx
xg
c)
)(
'xf
<
)(' xg
,với
;
2
1
)(
23
xxxf
xxxxg 2
2
1
3
2
)(
23
Lời giải:
a)
)(
'xf
< 0, với
xxxxf 6
2
5
3
1
)(
23
Ta có
65)( 2' xxxf
Mà
)(
'xf
< 0
Vậy tập nghiệm bất phương trình là: S=(2 ; 3)
32
065
2
x
xx
b)
0)(
'xg
,với
2
93
)(
2
x
xx
xg
Ta có
2
2
'
)2(
34
)(
x
xx
xg
Mà
0)(
'xg
2
1 x 3
x 4x 3 0 x 1;3 \ 2
x 2
x 2 0
Vậy tập nghiệm bất phương trình là: S=[1 ; 3]\2
c)
)(
'xf
<
)(' xg
, với
;
2
1
)(
23
xxxf
xxxxg 2
2
1
3
2
)(
23
Ta có
xxxf 23)(
2'
,
22)(' 2 xxxg
Mà
)(
'xf
<
)(' xg
1202022232223
22222
xxxxxxxxxxx
Vậy tập nghiệm bất phương trình là: S=(-2 ; 1)
Nhận xét: Tùy thuộc vào đề bài ta tính được đạo hàm của
)(xf
và
)(xg
(nếu có) sau đó
đem thế vào điều kiện có được từ đề bài để tìm nghiệm của bất phương trình.
Luyện tập củng cố:
Bài tập 1: Tính đạo hàm các hàm số sau:
1)
3 2
5
3 2
x x
y x
ĐS:
21y x x
2)
3
2
2
5
x
xy
ĐS:
41
10 2
y x
3)
2 3 4
2 4 5 6
7
yx x x x
ĐS:
2 3 4 5
2 8 15 24
7
yx x x x
4)
2 3 2
5 (3 1) 15 5y x x x x
ĐS:
2
45 10y x x
Bài tập 2: Tính đạo hàm các hàm số sau:
1) y = (x3 – 3x )(x4 + x2 – 1)
2)
32
)5( xy
3)
)35)(1(
22
xxy
4)
23 1y x x
x
5)
3
2y x
6) y = ( 5x3 + x2 – 4 )5
7)
4 2
3y x x
8)
2
2 5
2
x
yx
9)
2
1
2 3 5
yx x
10)
76
2
xxy
11)
21 xxy
12)
1)1(
2
xxxy
13)
12
32
2
x
xx
y
14)
1 x
y1 x
D. BÀI TẬP TRẮC NGHIỆM KHÁCH QUAN.
Câu 1: Số gia của hàm số , ứng với: và là:
A. 19 B. -7 C. 7 D. 0
Câu 2: Số gia của hàm số theo và là:
A. B. C. D.
Câu 3: Số gia của hàm số ứng với số gia của đối số tại là:
A. B. C. D.
Câu 4: Tỉ số của hàm số theo x và là:
A. 2 B. 2 C. D. −
Câu 5: Đạo hàm của hàm số tại là:
A. 0 B. 2 C. 1 D. 3
Câu 6: Hàm số
1x
1x2
y
có đạo hàm là:
A. y/ = 2 B.
2
/
)1x(
1
y
C.
2
/
)1x(
3
y
D.
2
/
)1x(
1
y
Câu 7: Hàm số
x1
2x
y
2
có đạo hàm là:
A.
2
2
/
)x1(
x2x
y
B.
2
2
/
)x1(
x2x
y
C. y/ = –2(x – 2) D.
2
2
/
)x1(
x2x
y
Câu 8: Cho hàm số f(x) =
2
x1
x1
. Đạo hàm của hàm số f(x) là:
A.
3
/
)x1(
)x1(2
)x(f
B.
3
/
)x1(x
)x1(2
)x(f
C.
2
/
)x1(x
)x1(2
)x(f
D.
)x1(
)x1(2
)x(f /
Câu 9: Đạo hàm của hàm số trên khoảng là:
A. B. C. D.
Câu 10: Đạo hàm của hàm số là:
A. B.
C. D.
Câu 11: Đạo hàm của hàm số là:
A. B.
C. D.
có thể bạn quan tâm
Đề thi thử THPT Quốc gia 2019 môn Toán cụm chuyên môn 01 – sở GD và ĐT...
0
730
319
Tài liệu, đề thi THPT các trường
(New)
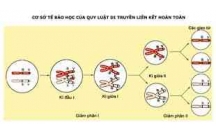
TÀI LIỆU ÔN THI TỐT NGHIỆP THPT QUỐC GIA:CHUYÊN ĐỀ: LIÊN KẾT GEN VÀ HO...
18
778
352
Tài liệu, đề thi Sinh Học
18
(New)
TÀI LIỆU ÔN THI TỐT NGHIỆP THPT QUÓC GIA MÔN SINH HỌC Chuyên đề: CƠ CH...
14
1.171
340
Tài liệu, đề thi Sinh Học
14
(New)
Tài liệu ôn thi tốt nghiệp THPT Quốc gia môn Sinh học: Chuyên đề QUẦN...
9
841
359
Tài liệu, đề thi Sinh Học
9
(New)
Đề thi thử tốt nghiệp THPT lần 2 môn toán lớp 12 năm học 2016-2017 trư...
8
997
312
Tài liệu, đề thi môn Toán
8
(New)
Đề thi thử môn Toán 2018 THPT Quốc gia trường THPT chuyên Lam Sơn – Th...
22
1.073
348
Tài liệu, đề thi THPT các trường
22
(New)
Đề thi thử lần 3 mônToán THPT quốc gia năm 2018 trường THPT Chuyên Ngu...
6
1.886
280
Tài liệu, đề thi môn Toán
6
(New)
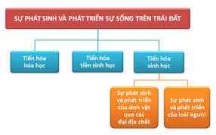
TÀI LIỆU ÔN TẬP THI THPT QUỐC GIA MÔN: SINH HỌC CHUYÊN ĐỀ: SỰ PHÁT SI...
6
1.018
424
Tài liệu, đề thi Sinh Học
6
(New)
thông tin tài liệu
Tài liệu gồm 28 trang Giới thiệu Lý thuyết về đạo hàm bào gồm các kiến thức cơ bản, kĩ năng cơ bản và bài tập vận dụng và các dạng câu hỏi trắc nghiệm có liên quan đến Đạo hàm.
Mở rộng để xem thêm
tài liệu mới trong mục này
Tài liệu ôn thi THPT Hóa học: 12 cách cân bằng phương trình hóa học
Tài liệu ôn thi THPT Môn Hóa học: CÁC DẠNG BÀI TẬP LUYỆN TẬP CÁC HALOGEN CLO
TÀI LIỆU ÔN THI THPT HÓA HỌC: PHẢN ỨNG OXI HÓA - KHỬ
Đề thi thử THPT môn Địa lý TRƯỜNG THPT YÊN LẠC 2 Vĩnh Phúc
TÀI LIỆU ÔN THI THPT QUỐC GIA MÔN ĐỊA LÝ: TỔNG HỢP 40 CÂU TRẮC NGHIỆM ĐỊA LÝ VIỆT NAM (CÓ ĐÁP ÁN)
tài liệu hot trong mục này
Đề thi thử THPT quốc gia môn Ngữ văn năm 2018 trường PTDTNT - Tuyên Quang (Lần 3)
Đề kiểm tra giữa kỳ 1 Toán 12 năm học 2018 – 2019 trường THPT Nhân Chính – Hà Nội
Tài liệu tổng hợp ôn thi THPT quốc gia lớp 12 môn Ngữ Văn
Đề thi Toán THPT quốc gia năm 2018 - mã đề 102
Tuyển tập 20 đề thi đọc hiểu luyện thi THPT Quốc gia môn Ngữ văn
tài liệu giúp tôi
Nếu bạn không tìm thấy tài liệu mình cần có thể gửi yêu cầu ở đây để chúng tôi tìm giúp bạn!
×
